In the previous section, we saw a circuit using one J-K flip-flop that counted backward in a two-bit binary sequence, from 11 to 10 to 01 to 00. Since it would be desirable to have a circuit that could count forward and not just backward, it would be worthwhile to examine a forward count sequence again and look for more patterns that might indicate how to build such a circuit.
Since we know that binary count sequences follow a pattern of octave (factor of 2) frequency division, and that J-K flip-flop multivibrators set up for the “toggle” mode are capable of performing this type of frequency division, we can envision a circuit made up of several J-K flip-flops, cascaded to produce four bits of output. The main problem facing us is to determine how to connect these flip-flops together so that they toggle at the right times to produce the proper binary sequence. Examine the following binary count sequence, paying attention to patterns preceding the “toggling” of a bit between 0 and 1:

Note that each bit in this four-bit sequence toggles when the bit before it (the bit having a lesser significance, or place-weight), toggles in a particular direction: from 1 to 0. Small arrows indicate those points in the sequence where a bit toggles, the head of the arrow pointing to the previous bit transitioning from a “high” (1) state to a “low” (0) state:

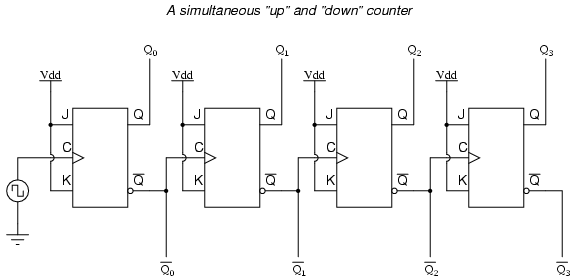
Starting with four J-K flip-flops connected in such a way to always be in the “toggle” mode, we need to determine how to connect the clock inputs in such a way so that each succeeding bit toggles when the bit before it transitions from 1 to 0. The Q outputs of each flip-flop will serve as the respective binary bits of the final, four-bit count:
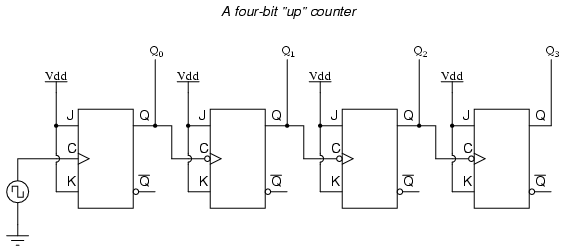
If we used flip-flops with negative-edge triggering (bubble symbols on the clock inputs), we could simply connect the clock input of each flip-flop to the Q output of the flip-flop before it, so that when the bit before it changes from a 1 to a 0, the “falling edge” of that signal would “clock” the next flip-flop to toggle the next bit:
This circuit would yield the following output waveforms, when “clocked” by a repetitive source of pulses from an oscillator:
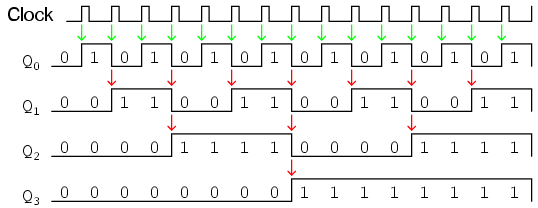
The first flip-flop (the one with the Q0 output), has a positive-edge triggered clock input, so it toggles with each rising edge of the clock signal. Notice how the clock signal in this example has a duty cycle less than 50%. I’ve shown the signal in this manner for the purpose of demonstrating how the clock signal need not be symmetrical to obtain reliable, “clean” output bits in our four-bit binary sequence. In the very first flip-flop circuit shown in this chapter, I used the clock signal itself as one of the output bits. This is a bad practice in counter design, though, because it necessitates the use of a square wave signal with a 50% duty cycle (“high” time = “low” time) in order to obtain a count sequence where each and every step pauses for the same amount of time. Using one J-K flip-flop for each output bit, however, relieves us of the necessity of having a symmetrical clock signal, allowing the use of practically any variety of high/low waveform to increment the count sequence.
As indicated by all the other arrows in the pulse diagram, each succeeding output bit is toggled by the action of the preceding bit transitioning from “high” (1) to “low” (0). This is the pattern necessary to generate an “up” count sequence.
A less obvious solution for generating an “up” sequence using positive-edge triggered flip-flops is to “clock” each flip-flop using the Q’ output of the preceding flip-flop rather than the Q output. Since the Q’ output will always be the exact opposite state of the Q output on a J-K flip-flop (no invalid states with this type of flip-flop), a high-to-low transition on the Q output will be accompanied by a low-to-high transition on the Q’ output. In other words, each time the Q output of a flip-flop transitions from 1 to 0, the Q’ output of the same flip-flop will transition from 0 to 1, providing the positive-going clock pulse we would need to toggle a positive-edge triggered flip-flop at the right moment:
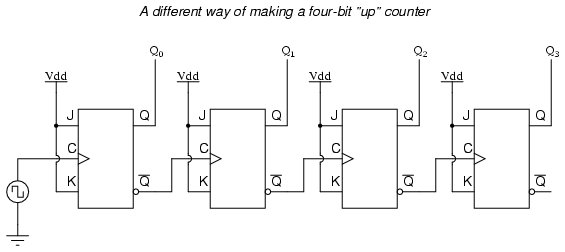
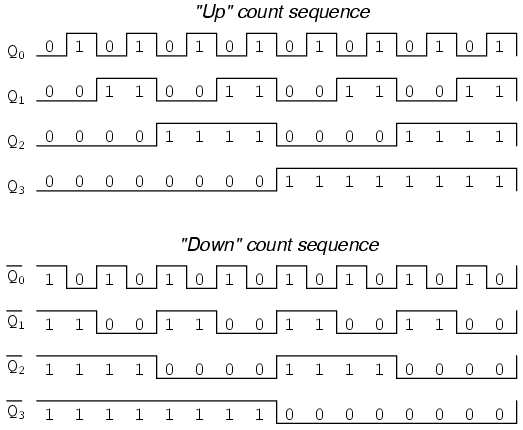
One way we could expand the capabilities of either of these two counter circuits is to regard the Q’ outputs as another set of four binary bits. If we examine the pulse diagram for such a circuit, we see that the Q’ outputs generate a down-counting sequence, while the Q outputs generate an up-counting sequence:
Unfortunately, all of the counter circuits shown thusfar share a common problem: the ripple effect. This effect is seen in certain types of binary adder and data conversion circuits, and is due to accumulative propagation delays between cascaded gates. When the Q output of a flip-flop transitions from 1 to 0, it commands the next flip-flop to toggle. If the next flip-flop toggle is a transition from 1 to 0, it will command the flip-flop after it to toggle as well, and so on. However, since there is always some small amount of propagation delay between the command to toggle (the clock pulse) and the actual toggle response (Q and Q’ outputs changing states), any subsequent flip-flops to be toggled will toggle some time after the first flip-flop has toggled. Thus, when multiple bits toggle in a binary count sequence, they will not all toggle at exactly the same time:
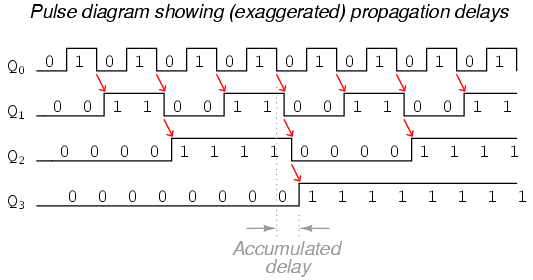
As you can see, the more bits that toggle with a given clock pulse, the more severe the accumulated delay time from LSB to MSB. When a clock pulse occurs at such a transition point (say, on the transition from 0111 to 1000), the output bits will “ripple” in sequence from LSB to MSB, as each succeeding bit toggles and commands the next bit to toggle as well, with a small amount of propagation delay between each bit toggle. If we take a close-up look at this effect during the transition from 0111 to 1000, we can see that there will be false output counts generated in the brief time period that the “ripple” effect takes place:
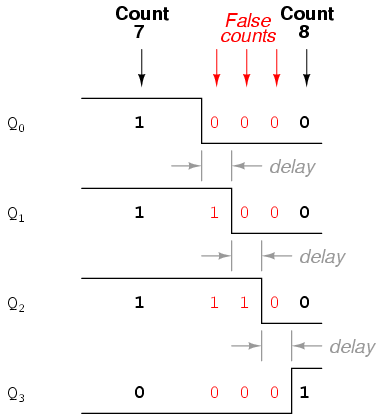
Instead of cleanly transitioning from a “0111” output to a “1000” output, the counter circuit will very quickly ripple from 0111 to 0110 to 0100 to 0000 to 1000, or from 7 to 6 to 4 to 0 and then to 8. This behavior earns the counter circuit the name of ripple counter, or asynchronous counter.
In many applications, this effect is tolerable, since the ripple happens very, very quickly (the width of the delays has been exaggerated here as an aid to understanding the effects). If all we wanted to do was drive a set of light-emitting diodes (LEDs) with the counter’s outputs, for example, this brief ripple would be of no consequence at all. However, if we wished to use this counter to drive the “select” inputs of a multiplexer, index a memory pointer in a microprocessor (computer) circuit, or perform some other task where false outputs could cause spurious errors, it would not be acceptable. There is a way to use this type of counter circuit in applications sensitive to false, ripple-generated outputs, and it involves a principle known as strobing.
Most decoder and multiplexer circuits are equipped with at least one input called the “enable.” The output(s) of such a circuit will be active only when the enable input is made active. We can use this enable input to strobe the circuit receiving the ripple counter’s output so that it is disabled (and thus not responding to the counter output) during the brief period of time in which the counter outputs might be rippling, and enabled only when sufficient time has passed since the last clock pulse that all rippling will have ceased. In most cases, the strobing signal can be the same clock pulse that drives the counter circuit:
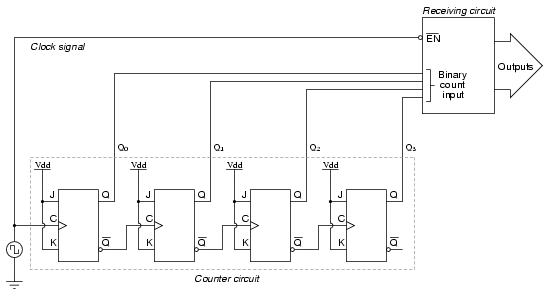
With an active-low Enable input, the receiving circuit will respond to the binary count of the four-bit counter circuit only when the clock signal is “low.” As soon as the clock pulse goes “high,” the receiving circuit stops responding to the counter circuit’s output. Since the counter circuit is positive-edge triggered (as determined by the first flip-flop clock input), all the counting action takes place on the low-to-high transition of the clock signal, meaning that the receiving circuit will become disabled just before any toggling occurs on the counter circuit’s four output bits. The receiving circuit will not become enabled until the clock signal returns to a low state, which should be a long enough time after all rippling has ceased to be “safe” to allow the new count to have effect on the receiving circuit. The crucial parameter here is the clock signal’s “high” time: it must be at least as long as the maximum expected ripple period of the counter circuit. If not, the clock signal will prematurely enable the receiving circuit, while some rippling is still taking place.
Another disadvantage of the asynchronous, or ripple, counter circuit is limited speed. While all gate circuits are limited in terms of maximum signal frequency, the design of asynchronous counter circuits compounds this problem by making propagation delays additive. Thus, even if strobing is used in the receiving circuit, an asynchronous counter circuit cannot be clocked at any frequency higher than that which allows the greatest possible accumulated propagation delay to elapse well before the next pulse.
The solution to this problem is a counter circuit that avoids ripple altogether. Such a counter circuit would eliminate the need to design a “strobing” feature into whatever digital circuits use the counter output as an input, and would also enjoy a much greater operating speed than its asynchronous equivalent. This design of counter circuit is the subject of the next section.
- REVIEW:
- An “up” counter may be made by connecting the clock inputs of positive-edge triggered J-K flip-flops to the Q’ outputs of the preceding flip-flops. Another way is to use negative-edge triggered flip-flops, connecting the clock inputs to the Q outputs of the preceding flip-flops. In either case, the J and K inputs of all flip-flops are connected to Vcc or Vdd so as to always be “high.”
- Counter circuits made from cascaded J-K flip-flops where each clock input receives its pulses from the output of the previous flip-flop invariably exhibit a ripple effect, where false output counts are generated between some steps of the count sequence. These types of counter circuits are called asynchronous counters, or ripple counters.
- Strobing is a technique applied to circuits receiving the output of an asynchronous (ripple) counter, so that the false counts generated during the ripple time will have no ill effect. Essentially, the enable input of such a circuit is connected to the counter’s clock pulse in such a way that it is enabled only when the counter outputs are not changing, and will be disabled during those periods of changing counter outputs where ripple occurs.