In the last section, we saw how the 3rd harmonic and all of its integer multiples (collectively called triplen harmonics) generated by 120° phase-shifted fundamental waveforms are actually in phase with each other. In a 60 Hz three-phase power system, where phases A, B, and C are 120° apart, the third-harmonic multiples of those frequencies (180 Hz) fall perfectly into phase with each other. This can be thought of in graphical terms, (figure below) and/or in mathematical terms:
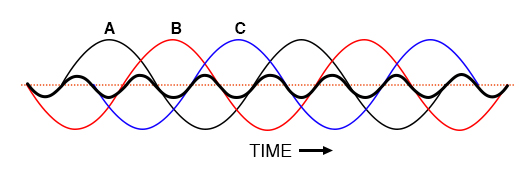
Harmonic currents of Phases A, B, C all coincide, that is, no rotation.
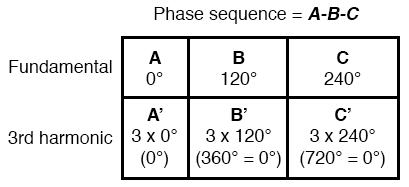
Extended Mathematical Table with Odd-Numbered Harmonics
If we extend the mathematical table to include higher odd-numbered harmonics, we will notice an interesting pattern develop with regard to the rotation or sequence of the harmonic frequencies:
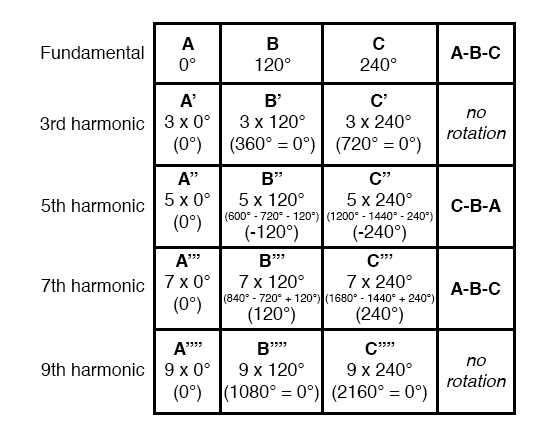
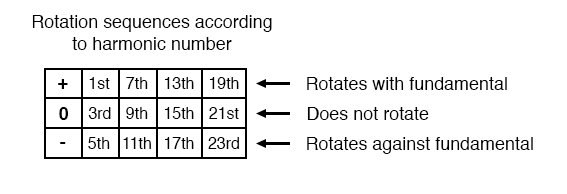
Harmonics such as the 7th, which “rotate” with the same sequence as the fundamental, are called positive sequence.
Harmonics such as the 5th, which “rotate” in the opposite sequence as the fundamental, are called negative sequence.
Triplen harmonics (3rd and 9th shown in this table) which don’t “rotate” at all because they’re in phase with each other, are called zero sequence.
This pattern of positive-zero-negative-positive continues indefinitely for all odd-numbered harmonics, lending itself to expression in a table like this: