Since transformers are essentially AC devices, we need to be aware of the phase relationships between the primary and secondary circuits. Using our SPICE example from before, we can plot the waveshapes for the primary and secondary circuits and see the phase relations for ourselves:
spice transient analysis file for use with nutmeg: transformer v1 1 0 sin(0 15 60 0 0) rbogus1 1 2 1e-12 v2 5 0 dc 250 l1 2 0 10000 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .tran 0.5m 17m .end nutmeg commands: setplot tran1 plot v(2) v(3,5)
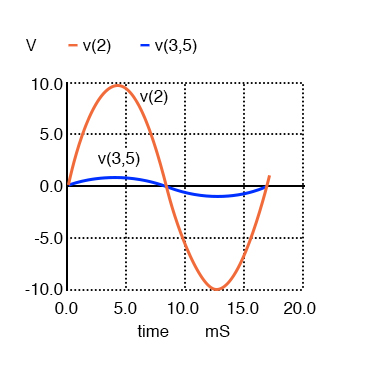
A secondary voltage V(3,5) is in-phase with primary voltage V(2) and stepped down by a factor of ten.
In going from primary, V(2), to secondary, V(3,5), the voltage was stepped down by a factor of ten, and the current was stepped up by a factor of 10. Both current and voltage waveforms are in-phase in going from primary to secondary.
nutmeg commands: setplot tran1 plot I(L1#branch) I(L2#branch)
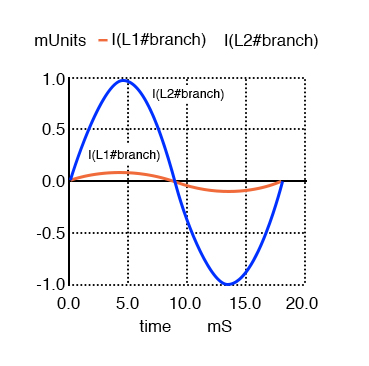
Primary and secondary currents are in-phase. Secondary current is stepped up by a factor of ten.
Transformer Conventions
It would appear that both voltage and current for the two transformer windings are in-phase with each other, at least for our resistive load. This is simple enough, but it would be nice to know which way we should connect a transformer in order to ensure the proper phase relationships be kept. After all, a transformer is nothing more than a set of magnetically-linked inductors, and inductors don’t usually come with polarity markings of any kind. If we were to look at an unmarked transformer, we would have no way of knowing which way to hook it up to a circuit to get in-phase (or 180° out-of-phase) voltage and current:
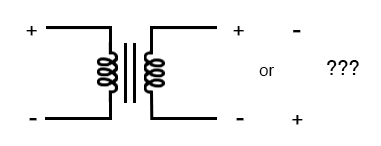
As a practical matter, the polarity of a transformer can be ambiguous.
Since this is a practical concern, transformer manufacturers have come up with a sort of polarity marking standard to denote phase relationships. It is called the dot convention, and is nothing more than a dot placed next to each corresponding leg of a transformer winding:
A pair of dots indicates polarity.
Typically, the transformer will come with some kind of schematic diagram labeling the wire leads for primary and secondary windings. On the diagram will be a pair of dots similar to what is seen above. Sometimes dots will be omitted, but when “H” and “X” labels are used to label transformer winding wires, the subscript numbers are supposed to represent winding polarity. The “1” wires (H1 and X1) represent where the polarity-marking dots would normally be placed.
The similar placement of these dots next to the top ends of the primary and secondary windings tells us that whatever instantaneous voltage polarity is seen across the primary winding will be the same as that across the secondary winding. In other words, the phase shift from primary to secondary will be zero degrees.
On the other hand, if the dots on each winding of the transformer do not match up, the phase shift will be 180° between primary and secondary, like this:
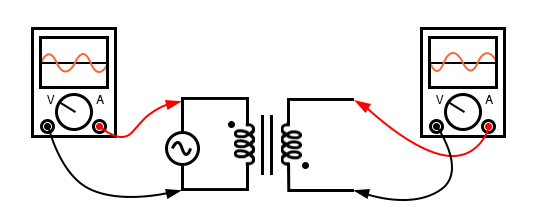
Out of phase: primary red to dot, secondary black to dot.
Of course, the dot convention only tells you which end of each winding is which, relative to the other winding(s). If you want to reverse the phase relationship yourself, all you have to do is swap the winding connections like this:
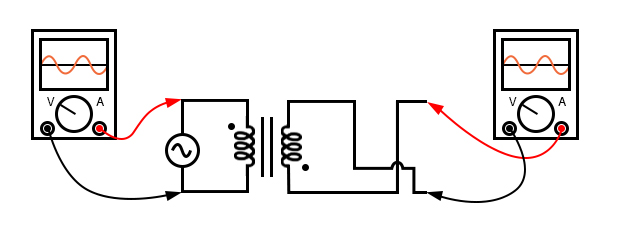
In phase: primary red to dot, secondary red to dot.
REVIEW:
- The phase relationships for voltage and current between primary and secondary circuits of a transformer are direct: ideally, zero phase shift.
- The dot convention is a type of polarity marking for transformer windings showing which end of the winding is which, relative to the other windings.